Seu mini guia de Lógica Proposicional
(Baseado em: MORTARI, Cezar A. Introdução à Lógica. 3. ed. São Paulo: Editora UNESP, 2001.)

Valores semânticos e Verocondicional
- Cada proposição pode assumir V (verdadeiro) ou F (falso).
- A interpretação de (i) atribui um valor a cada proposição:
* i (p) = V ou F
* i (q) = V ou F
* i (s) = V ou F
Conectivos Lógicos

Tabela de Verdade
Usadas para determinar o valor lógico de proposições compostas.
Passos:
- Identifique as proposições simples (p, q, r, s…)
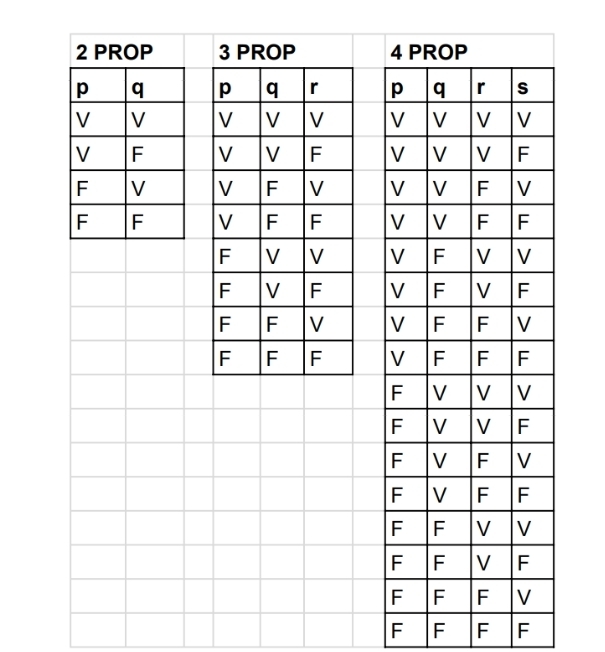
- Calcule o número de linhas: (n = número de proposições).
- Monte as colunas com todas as combinações de V e F.
Dica (caso você não tenha previamente o valor das proposições):
a) Na primeira coluna vai ser sempre metade V e metade F. Nas seguintes você começa a intercalar.
b) Ex, no caso de duas proposições, são quatro linhas. A primeira coluna fica: V , V , F , F. A segunda: V, F, V, F.
c) No caso de três proposições, serão oito linhas. A primeira coluna fica: V, V, V, V, F, F, F, F. A segunda fica: V, V, F, F, V, V, F, F.
d) E você vai replicando a lógica. (em breve, traremos mais informações, enquanto isso, segue a tabela a baixo para melhor compreensão)
4. Resolva de dentro pra fora, começando pelos parênteses.
5. Analise a última coluna:
só V → tautologia
só F → contradição
V e F → contingência
Tipos de Fórmulas

Exemplo de tabela completa:

- Observamos que é uma expressão contingênte. Pois apresentar valores verdadeiros e falsos.
Consequência Lógica (⊨)
Dizemos que uma proposição A é consequência lógica de um conjunto de proposições Γ (gama) quando:
Sempre que todas as proposições de Γ forem verdadeiras, A também é verdadeira.
- Em símbolos:
Γ ⊨ A
Lê-se: “A decorre logicamente de Γ”
ou
“A é consequência lógica de Γ”.
- Simplificando:
As proposições de Γ são as premissas.
A é a conclusão.
a) Se não existe nenhuma situação (ou linha da tabela) em que todas as premissas sejam verdadeiras e a conclusão seja falsa, então A é consequência lógica de Γ.
b) Se existe ao menos uma linha em que todas as premissas são verdadeiras e A é falsa, então A não é consequência lógica — e essa linha é o contraexemplo.
- Na prática (usando a tabela de verdade)
Para verificar se há consequência lógica:
1. Monte a tabela-verdade das premissas e da conclusão.
2. Observe todas as linhas em que as premissas são verdadeiras (V).
3. Veja o valor da conclusão nessas mesmas linhas:
Se for V em todas → ✅ Há consequência lógica.
Se for F em alguma → ❌ Há contraexemplo.
